关于Java中数据处理精度丢失的问题数值之间的转换
Java中经常需要将一种数值类型转换为另外一种数值类型,下图就给出了数值类型之间的合法转换。
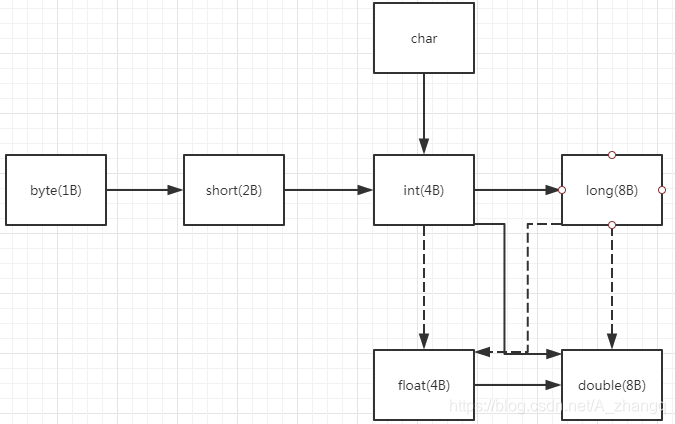
(图源)
实线代表合法转换即无信息丢失的转换,虚线表示转换可能存在精度丢失问题。
在进行两个数值的运算时,
如果两个操作数中有一个是double类型的,另外一个自动转换为double类型。
如果其中一个操作数是float类型的,另外一个操作数也将自动转换为float类型。
如果其中一个操作数是long类型的,另外一个操作数也将自动转换为long类型。
否则,两个操作数都会被转换为int类型。
所以在对两个不同类型操作数进行运算时,就可能存在精度丢失的问题。
例如:当一个int型数值和一个float型数值进行运算时,int型操作数将会自动转换为float型操作数。那么int型数值是如何转换为float型数值的?首先要了解他们是如何存储在计算机中的。整型在计算机中以第一位表示符号,剩余尾数表示数值的一串二级制数字来表示,而浮点型无论单精度还是双精度都有相同的存储方式:
符号位
指数位
尾数位
其中符号位表示浮点数的正负,指数位表示其的阶位,以移位的形势表现,尾数为表示其数值。其中float 1位符号位,8位指数位,23位尾数位。double 1位符号位,11位指数位,52位尾数位。
所以当一个int 类型的数值转换为float类型是,int型数值的32位拆分为 1位符号位,8位指数位,23位尾数位,改变了原本的表示方式,故产生了精度丢失。
其他的转换类似,当位数不够时通过补0来凑够位数。
java中double和float精度丢失问题
这是java和其它计算机语言都会出现的问题,下面我们分析一下为什么会出现这个问题:
float和double类型主要是为了科学计算和工程计算而设计的。他们执行二进制浮点运算,这是为了在广泛的数字范围上提供较为精确的快速近似计算而精心设计的。然而,它们并没有提供完全精确的结果,所以我们不应该用于精确计算的场合。float和double类型尤其不适合用于货币运算,因为要让一个float或double精确的表示0.1或者10的任何其他负数次方值是不可能的(其实道理很简单,十进制系统中能不能准确表示出1/3呢?同样二进制系统也无法准确表示1/10)。
浮点运算很少是精确的,只要是超过精度能表示的范围就会产生误差。往往产生误差不是因为数的大小,而是因为数的精度。因此,产生的结果接近但不等于想要的结果。尤其在使用 float 和 double 作精确运算的时候要特别小心。
现在我们就详细剖析一下浮点型运算为什么会造成精度丢失?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| 首先我们要搞清楚下面两个问题:
(1) 十进制整数如何转化为二进制数
算法很简单。举个例子,11表示成二进制数:
11/2=5 余 1
5/2=2 余 1
2/2=1 余 0
1/2=0 余 1
0结束 二进制表示为(从下往上):1011
这里提一点:只要遇到除以后的结果为0了就结束了,大家想一想,所有的整数除以2是不是一定能够最终得到 0。换句话说,所有的整数转变为二进制数的算法会不会无限循环下去呢?绝对不会,整数永远可以用二进制精 确表示 ,但小数就不一定了。
(2) 十进制小数如何转化为二进制数
算法是乘以2直到没有了小数为止。举个例子,0.9表示成二进制数
0.9*2=1.8 取整数部分 1
0.8(1.8的小数部分)*2=1.6 取整数部分 1
0.6*2=1.2 取整数部分 1
0.2*2=0.4 取整数部分 0
0.4*2=0.8 取整数部分 0
0.8*2=1.6 取整数部分 1
0.6*2=1.2 取整数部分 0
......... 0.9二进制表示为(从上往下): 1100100100100......
注意:上面的计算过程循环了,也就是说*2永远不可能消灭小数部分,这样算法将无限下去。很显然,小数的二进制表示有时是不可能精确的 。其实道理很简单,十进制系统中能不能准确表示出1/3呢?同样二进制系统也无法准确表示1/10。这也就解释了为什么浮点型减法出现了"减不尽"的精度丢失问题。
|
解决方法
使用《Effective Java》这本书中的BigDecmal,而且需要在构造参数使用String类型。
BigDecimal类有4个构造方法,但这里只关心对解决浮点型数据进行精确计算有用的方法,即
BigDecimal(double value) // 将double型数据转换成BigDecimal型数据
思路:先通过BigDecimal(double value)方法,将double型数据转换成BigDecimal数据,然后再正常进行精确计算了。计算完毕后,对结果做一些处理,比如:对除不尽的结果可以进行四舍五入。最后,再把结果由BigDecimal型数据转换回double型数据。
但是根据BigDecimal的详细说明,如果需要精确计算,不能直接用double,要用 String来构造BigDecimal。所以使用BigDecimal类的另一个方法,即能够帮助我们正确完成精确计算的 BigDecimal(String value)方法。
// BigDecimal(String value)能够将String型数据转换成BigDecimal型数据
那么问题来了:如果我们要做一个浮点型数据的加法运算,需要先将两个浮点数转为String型数据,然后用 BigDecimal(String value)构造成BigDecimal,之后要在其中一个上调用add方法,传入另一个作为参数,然后把运算的结果(BigDecimal)再转换为浮点数。如果每次做浮点型数据的计算都要如此,这个过程将非常繁琐,所以相对好的办法,就是写一个类,在类中完成这些繁琐的转换过程。这样在需要进行浮点型数据计算的时候,只要调用这个类就可以了。网上已经有大佬提供了一个工具类Arith来完成这些转换操作。它提供以下静态方法,可以完成浮点型数据的加减乘除运算和对其结果进行四舍五入的操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
| package com.util;
import java.math.BigDecimal;
public class Arith {
private static final int DEF_DIV_SCALE = 10;
private Arith() {
}
public static double add(double v1, double v2) {
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.add(b2).doubleValue();
}
public static double sub(double v1, double v2) {
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.subtract(b2).doubleValue();
}
public static double mul(double v1, double v2) {
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.multiply(b2).doubleValue();
}
public static double div(double v1, double v2) {
return div(v1, v2, DEF_DIV_SCALE);
}
public static double div(double v1, double v2, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b1 = new BigDecimal(Double.toString(v1));
BigDecimal b2 = new BigDecimal(Double.toString(v2));
return b1.divide(b2, scale, BigDecimal.ROUND_HALF_UP).doubleValue();
}
public static double round(double v, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b = new BigDecimal(Double.toString(v));
BigDecimal one = new BigDecimal("1");
return b.divide(one, scale, BigDecimal.ROUND_HALF_UP).doubleValue();
}
}
|
附上Arith的源代码,只要把它编译保存好,要进行浮点数计算的时候,在你的源程序中导入Arith类就可以使用以上静态方法来进行浮点数的精确计算了。
参考资料:
java中double和float精度丢失问题
https://blog.csdn.net/a_zhangq/article/details/90927472
